Lieke Voorintholt, University of Groningen, The Netherlands
How do people value the welfare of future generations? This question is of special importance now that the welfare of future generations is at stake because of expected climate change problems. This paper investigates people's preferences regarding intergenerational distribution of welfare. It discusses research on the time discounting of life saving and uses a new question that aims to measure the valuation of future generations' standard of life. Data is obtained from an online questionnaire (n = 138) and indicates decreasing valuation of future welfare. Heterogeneity is observed between distributions among one's descendants and among future generations in general. This might be explained by the superiority of either kinship-related or ethical motives that would differ for both sorts. Obtained distributions possibly reflect decreasing connectedness to generations over time until the point where such generations are considered strangers and no further discounting takes place. The effect of major life events such as grandparenthood also fit this explanatory framework. Changes in demographic factors could therefore translate to changes in intergenerational discounting. Exact predictions of these and other relationships should be confirmed by further research.
Keywords: Intergenerational discounting, societal preferences, kinship, ethics, economics of climate change.
Discounting is an economic subject serving many applications. The economic theory of cost–benefit analysis, for example, implies that decisions with delayed costs and benefits should be judged based on their net present value. This value is not only dependent upon present and future costs and benefits, but also on the unobservable social discount factor, which reflects society's valuation of some outcome taking place in the future relative to the present. Less explicit intergenerational discounting takes place continuously because both private and public consumption have implications for the very long run. An example of such an implication is climate change as a result of the emission of greenhouse gases. Since the climate tends to behave as a public good, climate change becomes a public policy issue for which the intergenerational discount factor is an important policy parameter.
Lower levels of discounting, exemplified by higher discount factors, imply a higher willingness to make sacrifices now in order to sustain the welfare level of future generations. Under the economic assumption that a benevolent social planner ideally uses policy parameters that reflect the values of citizens, it is crucial for governments to become familiar with the values of citizens regarding the topic of discounting. [i] The Economist thus states that decisions on the use of resources will ultimately be based on moral assumptions about how much less one values their descendants' lives than their own (The Economist, 2018). The reference to descendants rather than to future generations in general seems to correspond with widely expressed societal sentiments about how we will leave the earth to our children and grandchildren. Within-family intergenerational distribution preferences might, however, be based on very different motives than preferences for distribution among generations in general.
This paper compares 'private' discounting based on distribution preferences for one's own descendants to 'public' discounting based on such preferences for upcoming generations in general to obtain an indication whether separation of the two concepts is associated with different values and determinants. Data is collected to determine values for the two sorts of discounting based on a newly designed question. Moreover, this paper focuses not only on the factors associated with the two different sorts of intergenerational discounting, but also on the manner in which differences in respondents' background variables correlate with differences between their distribution preferences. This can potentially shed light on how intergenerational discounting is associated with major life events.
As mentioned before, the intergenerational discount factor is a crucial determinant of models that calculate how much consumption to forego now in order to limit future climate change. As a result, societal approval of an intergenerational discount factor that resembles the normative value of 1 would greatly contribute to preventing climate catastrophe. It would therefore be useful to obtain information about which background variables, if any, serve to explain the value of someone's intergenerational discount factor and whether private discounting differs from public discounting. The lack of empirical research still leaves many blanks in the understanding of intergenerational discounting. This paper finds that heterogeneity between discount factor values can be partially explained by the interplay between ethical and kinship-related motives that are triggered for certain distribution decisions.
Discounting of personal consumption has been subject to research for a long time, starting with the work of Fisher (1930). It should, however, be clarified that intergenerational discounting is distinct from the concept of consumer impatience, which forms the basis of such regular discounting within one's lifespan, especially the simple form of monetary discounting. The following critique by Schelling supports this idea:
The alleged inborn preference for earlier rather than later consumption is exclusively concerned with the consumer's impatience with respect to his or her own consumption. […] But greenhouse policy is not about saving for later consumption. It is about foregoing consumption in order that somebody else at a later time enjoys more consumption than would otherwise be available.
Intergenerational distribution where trade-offs are made between the welfare of future generations independent of personal welfare level can formally be captured in a theoretical model (Appendix A). This model can, in turn, be used for the interpretation of empirical findings of this paper.
Based on the literature, ethics and kinship appear to be the main motives that determine whether someone has a high or low discount factor. Before discussing these motives, this section will first reflect on the literature about time discounting life saving, which until now has most closely approached empirical measurement of intergenerational discounting.
Cropper et al. (1994) dominate research on long-term discounting derived empirically from measured individual choice. Using various participant pools, they repeated a 12–15-minute telephone survey in which respondents were asked whether they prefer a programme that saves a fixed number of lives now over a programme that saves a higher fixed number of lives in t years from now, where t varies from t = 5 to t = 100. They found that the constant exponential annual discount factor clearly increases with the length of the time horizon. Their general results are not always supported by outcomes of other studies of the same sort (Johannesson and Johansson, 1997; Frederick, 2003). Most other papers pose the critique that the manner in which the life-saving question is framed leads to highly varying results.
However insightful, the empirical research on life-saving discounting provides inadequate basis to draw valid conclusions about intergenerational discounting of welfare. Saving a number of lives is of a very different order than the broad and much less concrete consequences of current consumption and investment on future welfare. This paper therefore uses a different methodology for its results.
Various publications on intergenerational discounting – of which Stern's (2006) is most well-known – present a normative discount factor that is based on welfare economics' ethical framework of total utilitarianism. This sort of utilitarianism implies zero pure discounting, since equal weight should be given to the welfare of current and future people. When focusing on positive rather than normative economics, aggregated discount factors that are based on this view cannot simply be used as a representation of societal discounting preferences. What can be studied instead are the individuals who apply this sort of reasoning in their distribution decision, which is also what this paper attempts to do.
Following the quotation at the start of this section, Schelling makes the claim that he would have no preference for an increment of consumption to accrue in the year 2150 to strangers not yet existing compared to such an increment accruing in the year 2100 also to strangers not yet existing. Directly after, he admits that this might be different for preferences in the short term:
I can imagine reasons – some of them may even appeal to me – for preferring a boost to consumption in 2025 to the same boost of consumption in 2075 […] In 2025, my oldest son will be the age I am today and his brothers a little younger; with a little luck they will be alive and healthy and my grandchildren will be the ages that my children are today, and my great-grandchildren (whom I do not yet know) will have most of their lives ahead of them. Seventy-five years later they will all be strangers to me. My genes may be as plentiful in the population at the later date but they will be spread thinner.
Schelling uses the strength of a genetical connection to explain his potential time preference. Certain anthropologists have also defined kinship in American culture as biogenetic:
Because blood is a 'thing' and because it is subdivided with each reproductive step away from a given ancestor, the precise degree to which two persons share a common heredity can be calculated, and 'distance' can thus be stated in specific quantitative terms.
For descendants, genetic relatedness exponentially decreases with factor 0.5 per generation. Since low levels of relatedness stretch over infinitely many generations, Schneider suggests that in American society, the level of relatedness that is still associated with kinship is a personal decision. Data on actual distribution decisions among multiple generations of descendants could provide insight on such 'cut-off points'. A first indication of such a point might be the focus on the futures of one's children and grandchildren, which is more common in the public conversation on climate change, than the focus on the future of one's complete set of future offspring.
Kinship can obviously also occur in other forms than the one based on Schneider's model that relates it to genetical connections. As a result, the people who fully base their discount factors on kinship-related motives might not necessarily value their grandchild's welfare factor 0.5 of the welfare of their child. Naturally, ethical and kinship-related motives can also be mixed, leading to less extreme outcomes.
A first hypothesis is that the influence of total utilitarian motives that speak for an equal distribution of welfare will be most prevalent in the broader societal context of distribution between generations in general. This implies that, on average, public discounting will be lower than private discounting. Additional regression results that would fit this explanatory framework imply that non-societal individual characteristics of respondents have less of an effect on the public than on the private discount factors. The climate impact proxies number of new clothes and number of new flights are hypothesised to lower the average public discount factor π.
Second, along the same line of reasoning, kinship-related motives will be stronger when distribution only takes place among one's own descendants. Moreover, the kinship-related motives might be more influential for those generations of descendants with whom a social connection is experienced strongest and before the cut-off point that was mentioned before. In terms of regression results, this framework predicts that grandparents will have a higher value of the proxy used for valuation of one's grandchild's welfare than non-grandparents do of potential grandchildren's. In addition, people who might have known more members further up their family tree such as great-grandparents will also feel a stronger connection to a (potential) descendant that is similarly distant (one's great-grandchild in this case).
Since there exists no suitable dataset to answer the research questions of this paper, own data was collected. This was done with the use of a questionnaire study, which allows for the possibility to research the relationships between a large number of variables.
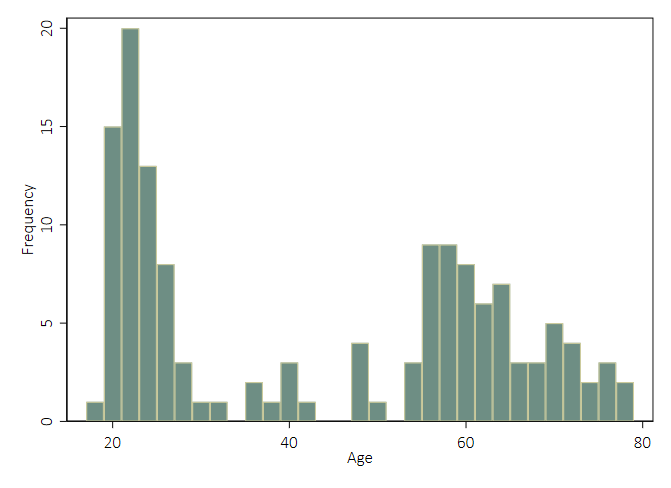
Research participants are Dutch adults of ages 18 to 78 (M 43.0, Mdn 44.5). However, as can be observed in Figure 1, the sample shows a clear peak for 20-year-olds (Mode 22) and a relatively small number of participants between the ages 30 to 50. This might be caused by the use of a convenience rather than a random sample. The total number of respondents is 138, of which 65 are females and 73 are males. Their median income interval is €2000–€2999 net per month. Of the total respondents, 63 are parents, of whom 48 have children over 19 years of age, and 34 of these respondents are grandparents.

The 138 responses were collected between 26 March to 15 April 2019. During this period, an online questionnaire was distributed to acquaintances of the author through Facebook, e-mail and by individual requests. Awareness exists that both the relatively small sample size and the manner in which respondents were selected can lead to biased outcomes. The conclusion of this paper further addresses this issue.
An online questionnaire was created with a total of 33 questions in Dutch. The questionnaire contained many questions that aim to measure relevant background variables to include in the regression – from basic demographics to numbers of family members of various categories. In the cases of parents,[ii] grandparents and great-parents, respondents were asked for the number of these family members that they have memories of (not just on the basis of pictures). The questionnaire ended with questions on relevant behavioural variables such as smoking,[iii] new clothing consumption, plane travelling and volunteering. Furthermore, respondents' life-saving discount factors were measured with a question in line with previous research. The results of this will not be discussed in this paper.
Intergenerational distribution preferences were measured with the use of a self-designed question (Appendix B), which is the most important section of the questionnaire. This question asks for the distribution of 100 lottery tickets over five future generations. Each lottery ticket represents a per cent chance on an equal or higher standard of life than one's own. The lottery ticket distribution over generations of one's descendants (private discounting) can be compared to the distribution over generations in general (public discounting). It needs to be mentioned that the use of a lottery in the hypothetic situation potentially influences results because it introduces risk preferences that can impact time preferences in some cases (Andreoni and Sprenger, 2012).[iv]
Respondents were asked to distribute standard of life rather than utility or broad consumption (including non-monetary goods and services), because those concepts might be difficult to understand for non-economists. The standard of life is suitable because it does not end up on top of a certain standard that the future generation is already expected to have, but fully determines that standard. The level of the standard of life that respondents could distribute is their own, such that no value had to be specified.
The standard of life is defined in the questionnaire as a combination of multiple definitions found on the internet (Statistics Netherlands, 2014; Fontinelle, 2019) in the following manner:
The standard of life gives an indication of the level of human welfare on economic, social and cultural dimensions. Various indicators are used to measure the level of the standard of life. Think of material resources, the structure of society (housing, education and health care, etc.) and the (natural) environment, for example.
Discount factors can be calculated based on the outcomes of the private and public intergenerational distribution question using the following expression:  .
.
The number of lottery tickets distributed to Generation g+1 as a share of the lottery tickets distributed to Generation g captures a respondent's implicit valuation of the standard of life of a generation in terms of the standard of life of the previous generation. To convert this to a yearly discount factor, the shares simply have to be raised to the power 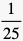 , where 25 indicates the number of years between two generations according to the question that respondents faced. Applying this calculation to the five answers on the two questions corresponding to both cases results in a total of eight discount factors. δi corresponds to the generation intervals between descendants and πi corresponds to the generation intervals between future generations in general (i = 1, 2, 3, 4). Both sets of factors have their own 'time-invariant' discount factor δ and π, which is the average of the four factors that are each specific to a combination of two subsequent generations.
, where 25 indicates the number of years between two generations according to the question that respondents faced. Applying this calculation to the five answers on the two questions corresponding to both cases results in a total of eight discount factors. δi corresponds to the generation intervals between descendants and πi corresponds to the generation intervals between future generations in general (i = 1, 2, 3, 4). Both sets of factors have their own 'time-invariant' discount factor δ and π, which is the average of the four factors that are each specific to a combination of two subsequent generations.
Figure 2 represents a visualisation of intergenerational distribution that is based on lottery ticket distribution (among future generations in general). The number of tickets of the generation in each box equals that of the generation above multiplied with the yearly discount factor raised to the power number of years between the two generations (see arrows).
Econometric techniques
The normal distribution of most variables was tested with the Skewness-Kurtosis test. The outcome of non-normality implies the use of median rather than mean comparison. Therefore, the Wilcoxon Signed-Rank test was used to compare medians of two measures with one sample.[v] To test hypotheses about regression coefficients, a multivariable regression with several of the discount factors δ and π as dependent variables was performed on the data using robust standard errors. Significance of the regression coefficients was determined using t-tests.
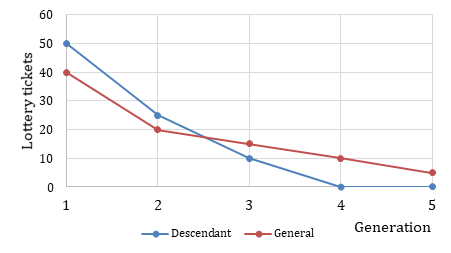
Figure 3 gives a first impression of empirical results. The line graph clearly shows a wider range of median lots distributed to descendants than to generations in general, with the final two median values of the former even equalling zero. Median comparisons indicate that a higher number of lottery tickets was given away to the first two generations of descendants than the first two generations in general (p = 0.000). Another main difference between the two distributions is the discounting that takes place between Generations 2 and 3. The discount factor appears to be much lower for private than for public distribution: δ2 < π2. Clearly, this had to happen at some point because the two distribution graphs cross at least once by construction.
Summary statistics of the discount factors are presented in Tables 1 and 2. No factors could be calculated for a combination of Generations g+1 and g if the number of lottery tickets distributed to Generation g is zero. The lower variable count of the δi's than πi's indicates that this turns out to be the case more often for private than public discounting.
The median overall private discount factor δ = 0.66 is lower than the median public discount factor π = 0.98 (p = 0.000). In fact, this holds for all δi and πi except for i = 4, which shows that higher private than public discounting is present but not limited to the earlier generations where close descendant ties still distinguish the two sorts of distribution. The pattern does not hold anymore for δ4 and π4. The median value of 1 for both factors indicates a halt to discounting after four generations (≈ 100 years). The median discount factor π3 is also 1, which indicates a halt to discounting already at an earlier stage than in the case of distribution among descendants. The self-designed question should have included a sixth generation to distribute lottery tickets to in order to find stronger evidence of a halt to discounting.
The pure kinship effect of a genetical connection with a descendant is associated with a value loss of factor 0.5 per generation. As the self-designed question assumed a 25 year time period between each generation, the annual discount factor corresponding to the factor 0.5 is approximately 0.9727.[vi] This is exactly the median value of δ2. This value is significantly smaller than δ1, δ3 and δ4, which means that the level of (constant exponential) discounting is thus the highest between one's grandchild and great-grandchild. However, a similar pattern holds for public discounting as indicated by the factors πi. Apparently, relatively most value is lost after two generations. This is exactly in line with the all-too-common reference to 'the future of our children and grandchildren' used in the public conversation on climate change. The increase in discounting of the welfare of Generation 3 corresponds to using the generation of one's great-grandchildren as a 'cut-off point'.
| δ1 | δ2 | δ3 | δ4 | δ | |
| median | 0.9839 | 0.9727 | 0.9862 | 1 | 0.6576 |
| mean | 0.8382 | 0.7214 | 0.7705 | 0.9217 | 0.6717 |
| sd | 0.3513 | 0.4354 | 0.4131 | 0.2640 | 0.3521 |
| N | 135 | 117 | 86 | 67 | 137 |
| π1 | π2 | π3 | π4 | π | |
| median | 0.9886 | 0.9839 | 1 | 1 | 0.9762 |
| mean | 0.8626 | 0.7964 | 0.8253 | 0.8859 | 0.7226 |
| sd | 0.3291 | 0.3918 | 0.3714 | 0.3183 | 0.3438 |
| N | 135 | 119 | 96 | 80 | 136 |
As a robustness check, discount factors based on a different number of years between two generations are calculated and compared to the default of 25 years. For all factors except δ2, the differences for t = 20 and t = 30 are less than 0.01. Although no reason for immediate concern, a difference of 0.01 should still be regarded as important if the factors would be used for (policy) implementations. To illustrate, the half-life corresponding to π = 0.97 is 23 years, whereas it is 34 years for π = 0.98.
Table 3 presents a total of five regressions: three for private discount factors and two for public discount factors as dependent variables. All regression models for the other discount factors turned out to be insignificant as a whole based on their F-statistics. Right-hand sides of the regression equations contain several background variables that were measured in the questionnaire, some of which were transformed to dummies. The following paragraphs will point out the most remarkable results and reflect on ideas posed in the conceptual framework. A first remark is that only a minority of independent variables turns out to significantly explain the dependent variables.
Both the private and public discounting models show a negative effect of the male gender on the discount factor. This effect is significant for δ2, where the discount factor of males is on average 0.22 lower than of females. This means that males discount the welfare of their great-grandchildren relative to the welfare of their grandchildren much more than females do, ceteris paribus. The number of siblings shows a significant negative effect on δ2 for which no immediate explanation can be given as well.
Significance of βGrandchildren > 0 for δ1 means that a person who has grandchildren discounts their grandchild's welfare relative to their child's much less than a person without grandchildren, ceteris paribus. No such effect is found for the factor δ2 that indicates the same relationship for the jump from one's grandchild to great-grandchild. In contrast, its beta-coefficient has a negative sign and even larger absolute value (but is insignificant). This does not necessarily indicate that grandparents care less about their great-grandchildren than do non-grandparents, but rather that they have given away a higher number of lottery tickets to their grandchildren in comparison and therefore have to decrease that number with a higher percentage. This might also serve as an explanation for δ2 as minimum discount factor. The grandchildren effect is not significant in the case of public discounting, which confirms the idea that kinship-related effects are less prevalent for this more societal sort of discounting.
The number of grandparents that one has known does not significantly explain either the private or the public discount factors, although this variable was expected to positively correlate with the discount factor δ1. A similar conclusion can be drawn about great-grandparents and the expected positive relationship with δ2.
With regard to behavioural variables, the expected negative effect on π is significant for Flights, but not for New clothes. Both variables have a negative impact on the discount factor for all cases, which is in line with the idea that high consumption of goods or services that are associated with negative externalities is related to a lower reflection of ethical motives in one's discount factor. Volunteering, which is instead associated with positive rather than negative externalities, has a positive sign and is significant for some of the models instead.
Finally, income shows a negative effect on the discount factor in all cases, indicating higher discounting. A higher income, therefore, points to 'short-sightedness' in the case of intergenerational distribution. Significance, however, only holds for δ2 (using α = 0.05).
| Dependent variable | δ1 | δ2 | δ | π1 | π |
| Male | -0.0840 | -0.2153* | -0.1132 | -0.0920 | -0.1188~ |
| (0.185) | (0.027) | (0.101) | (0.150) | (0.084) | |
| Age | -0.0102 | 0.0050 | -0.0075 | 0.0135 | 0.0039 |
| (0.550) | (0.829) | (0.660) | (0.438) | (0.812) | |
| Age Squared | 0.0000 | 0.0000 | 0.0000 | -0.0002 | -0.0001 |
| (0.950) | (0.868) | (0.878) | (0.264) | (0.672) | |
| Income | -0.0193 | -0.1257** | -0.0499 | -0.0307 | -0.0483 |
| (0.558) | (0.003) | (0.103) | (0.341) | (0.130) | |
| Siblings | -0.0058 | -0.0561* | -0.0218 | -0.0050 | -0.0137 |
| (0.725) | (0.041) | (0.112) | (0.752) | (0.356) | |
| Childrena | 0.0763 | 0.0535 | 0.0645 | -0.0907 | -0.0802 |
| (0.668) | (0.763) | (0.681) | (0.538) | (0.602) | |
| Grandchildrena | 0.3511* | -0.2196 | 0.1535 | 0.1937 | 0.0605 |
| (0.027) | (0.280) | (0.236) | (0.239) | (0.641) | |
| Grandparents known | -0.0042 | 0.0409 | 0.0070 | 0.0083 | 0.0179 |
| (0.877) | (0.391) | (0.786) | (0.772) | (0.486) | |
| Great- grandparents known | 0.0434 | -0.0619 | -0.0091 | -0.0507 | -0.0676 |
| (0.243) | (0.272) | (0.829) | (0.307) | (0.156) | |
| Volunteering hoursb | 0.0014~ | -0.0011 | 0.0011 | 0.0021* | 0.0018~ |
| (0.052) | (0.638) | (0.384) | (0.028) | (0.057) | |
| New clothesb | -0.0252 | -0.0031 | -0.0215 | -0.0230 | -0.0151 |
| (0.105) | (0.799) | (0.119) | (0.114) | (0.274) | |
| Flightsc | -0.0099* | -0.0016 | -0.0074 | -0.0124** | -0.0107* |
| (0.044) | (0.879) | (0.110) | (0.010) | (0.017) | |
| Constant | 1.3172** | 0.9912** | 1.1715** | 0.9290** | 0.9885** |
| (0.000) | (0.008) | (0.000) | (0.000) | (0.000) | |
| N | 120 | 102 | 122 | 120 | 121 |
| R2 | 0.286 | 0.292 | 0.288 | 0.251 | 0.297 |
|
Two-tailed p-values in parentheses ~ p < 0.10, * p < 0.05, ** p < 0.01 a: the variables Children and Grandchildren are dummy's for having at least one family member in this category b: the variables Volunteering hours and New clothes are measured per month c: the variable Flights measures the number of plane flights over the past two years |
|||||
Intergenerational discounting shows much heterogeneity. For some respondents, a cut-off point after which they distribute 0 tickets can be observed after one or two generations, whereas some others perfectly equally distribute all tickets over the five generations. Overall statistics show that private distribution among one's descendants is associated with higher discounting than public distribution among generations in general. Both distributions show a clear decreasing trend and discount factors still lie within a narrow range. Small differences in the exact height of a discount factor can however lead to very different outcomes.
Kinship effects, assuming they generally lead to higher discounting, thus seem to be triggered by the reference to descendants. A more explicit trigger of kinship effects, specifically on discount levels surrounding the generation of one's grandchild, is whether one has grandchildren. Grandparents probably experience a higher perception of social connectedness to this generation. However, something that is not in line with the hypotheses of this paper is the very insignificant effect of number of grandparents and great-grandparents that one has known on discounting. This indicates that relational ties with ancestors have no significant impact on distribution and discounting choices. The experience with family members of distant generations apparently only affects the strength of kinship-related motives future generations of similar distance if those family members are or were descendants rather than ancestors.
Instead of a clear cut-off point where the number of distributed lottery tickets falls to zero, median values seem to indicate that when two generations are considered similarly distant the discount factor will take on the value 1. As specified by the theoretical model, this implies that both Generations g and g + 1 are valued equally by the individual in Generation 0.
Consumption of clothing garments and plane flights that are associated with negative externalities are also indicative of lower discount factors. The opposite holds for volunteering. Assuming that imposing positive or negative externalities on society is related to relative importance of ethical motives that speak for equal distribution, this result fits the hypothesised framework in which the relative importance of motives is based on certain triggers that can be proxied by basic background variables.
This paper has presented a very explorative sort of research. The new empirical measurement of discount factors might, however, be a welcome addition to the discipline of climate economics in which discount factors presented are – most of the time – either normative or based on concepts that do not appear representative of intergenerational distribution preferences. The interplay between ethical and kinship-related motives can serve as an explanation of heterogeneity in discount factors. The results of this paper, therefore, seem meaningful and worth further research.
Awareness exists of the fact that the methodology has several limitations. Trade-off between own and future welfare was not perfectly mirrored in the question on lottery ticket distribution, which did not require respondents to include themselves in the distribution decisions. In the extreme case where the valuation of a future beyond one's death is zero, intergenerational discounting preferences beyond one's death are not even relevant. This limitation is however also applicable to life-saving questions, where lives saved are most likely those of distant strangers and do not have anything to with foregoing own consumption of either healthcare or material goods. In the case of lottery ticket distribution, these very short-sighted people might distribute all of their 100 tickets to Generation 1. In that case their high discounting preferences are still revealed.
Another important and more practical limitation has been the use of a convenience sample rather than a randomised sample. This might have especially limited the outcomes of the regression models that would have moreover profited from both a higher sample size and a more heterogeneous sample. The perceived difficulty of the questionnaire increased the difficulty of finding respondents. From the 138 respondents there were still many who, based on their illogical answers, misinterpreted the life-saving and monetary discounting questions.
In line with the final limitation raised, the most important step forward is optimisation of the intergenerational distribution question. The question should be further simplified to stimulate response rates and additional generations could be added to investigate the potential halt to discounting. Finally, it needs to be presented to a larger and randomised sample, for instance the LISS panel (Longitudinal Internet Studies for the Social sciences). This is a representative sample of true probability of Dutch households drawn from the population register (Scherpenzeel and Das, 2010).
New variables could be used to investigate 'triggers' of kinship. For example, instead of using a dummy for having (had) grandchildren, the number of grandchildren or the perceived quality of the relationship could be used as variables. In addition to grandparenthood, the effect of great-grandparenthood can be tested with a representative sample that includes great-grandparents. Similarly, new variables that capture the strength of the ethical motive could be included.
Finally, follow-up research would profit from a new set of analysis procedures that might make interpretation of results somewhat more straightforward. Although it would disregard variation between discount factors corresponding to different combinations of generations, a single time-invariant discount factor would be a great addition to other statistics. The fit of other discount functions than a constant exponential function, such as a quadratic or linear function should in that case also be tested. Especially with the apparent halt to discounting after 3 or 4 generations, it seems suitable to use a different sort of function than the default of constant exponential discounting used in the neoclassical theory of project evaluation (Arrow and Kurz, 1970).
Further confirmation of high discount factors would show the need of governments to act upon this valuation in such a manner that desired future welfare levels can still be attained. An example is implementing model outcomes based on the factors, for instance a carbon tax (Pindyck, 2013; Poelhekke, 2017).
Deciding on the right discount factor 'requires a fundamental decision about how much we care about future generations' (Partnoy, 2012: 240). Slowly but certainly more researchers, journalists and politicians seem to become aware of this importance. Because of the involved irreversibility it is crucial that citizens will take over this awareness and continue, or start, to think about discounting beyond death.
Figure 1: Histogram for respondent age
Figure 2: A model of intergenerational distribution
Figure 3: Median values of lottery tickets distributed
Table 1: Summary statistics of the private discount factors
Table 2: Summary statistics of the public discount factors
Table 3: Regression models for private and public discount factors
A formal theoretical model can be constructed to provide economic intuition for the results that will be presented later in this paper. Consider an individual in Generation 0 who values the utility of the two generations following his own: Generations 1 and 2. His own utility U0 is then a function of the utility levels of Generation 1 and Generation 2. Assume that U1 does not enter U2 and vice versa. The expected utility of these two generations is, however, determined by the number of lottery tickets they receive, which indicates each generation's chance on a high standard of life. The methodology section provides a full explanation of this hypothetical situation. For Generation 1 the number of lottery tickets is L, and for Generation 2 it is 100 - L, where 100 indicates the total number of lottery tickets available:
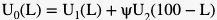
This individual therefore maximises his utility by allocating the 100 tickets such that the additional utility he would receive from giving an additional ticket to Generation 1 is identical to the additional utility he would receive if he would give it to Generation 2 instead. That is, we have the following first-order-condition that needs to hold in equilibrium:
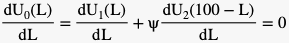
From which it follows that:
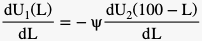
and:
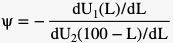
Where Ψ indicates the valuation of the utility of Generation 2 as a factor of the utility of Generation 1.
The assumption is made that Generation 1 and Generation 2 will equally enjoy chance on a high standard of life measured by lottery tickets: U1(L) = U2(100 - L). In this case, an unequal distribution of lottery tickets points out that Ψ ≠ 1. If Ψ < 1, the individual from Generation 0 has a preference to distribute a majority of lottery tickets to Generation 1. If instead Ψ > 1, distributing a majority of lottery tickets to Generation 2 is preferred. This is called 'negative discounting'.
This model can be extended to more than two future generations, but the intuition remains the same.
This question is about how important you deem it that (your potential own descendants/upcoming generations in general) will have the same standard of life as you have or expect to have during the rest of your life.
Imagine that each (of your descendants/generation) participates in their own 'standard of life lottery'. Each lottery has 100 participating lottery tickets and the different lotteries operate independently of one another. Each lottery will draw one winning lottery ticket. The prize for the winning ticket in each lottery is the same or a higher standard of life than (your own/that of your own generation). Thus, for each (descendant/generation) every additional lottery ticket equals an extra per cent change on winning this price
You can decide the number of lottery tickets that each (descendant/generation) will receive to participate in his or her own lottery. You have a total of 100 lottery tickets to divide over (your (potential) descendants/the five generations following yours). Assume that each (descendant/generation) will get one child at age 25 and that everyone's life expectancy at birth is 85 years.
Example: Assigning 100 lottery tickets to a descendant (generation) means that the winning lottery ticket will always be in the possession of this descendant (generation) and he/she will thus always have the same or a higher standard of life than yourself. Assigning 0 lottery tickets to a descendant (generation) means that the winning lottery ticket will in no occasion be in the possession of this descendant (generation) and he/she will thus always have a lower standard of life than yourself. Each number of lottery tickets in-between these two extremes will not provide complete security about the standard of life of the descendant (generation.) With 30 lottery tickets, the descendant (generation) has 30 per cent chance of the same or a higher standard of life than yours.
Indicate your desired distribution below:
(Child/1 generation following yours): _______
(Grandchild/2 generations following yours): _______
(Great-grandchild/3 generations following yours): _______
(Great-great-grandchild/4 generations following yours): _______
(Great-great-great-grandchild/5 generations following yours): _______
[i] This is an extensive discussion point in the work of Dasgupta (2001).
[ii] In a later stage, the variable Parents was excluded from the regression completely. Many people filled in a value that was higher than two, which probably referred to their stepparents as well. However, the idea of this question was not to compare the impact of having stepparents on discount factors. It was merely meant as a control and for completeness, but no effect was expected. Due to the expected misinterpretation, it was decided to simply exclude the variable.
[iii] In a similar manner, the independent variable Smoker was dropped due to a very small percentage of smokers (of which some also only light smokers). It was originally included to check whether the same significant negative relationship between cigarette consumption and the life-saving discount factor was found as by Cairns (1994).
[iv] However, these authors also state that the influence appears to be limited in the case when uncertainty is equal for the complete choice set. The lottery still appears a suitable instrument for the questionnaire, because it allows for the incorporation of the binary outcome 'same or higher/lower standard of life' rather than the 'share' of one's own standard of life. With the current method used there is no need to specify how much lower a lower standard of life is, so that distribution decisions are less extreme and more realistic.
[v] This test considers the relative magnitude as well as the direction of differences between the two measures (Siegel, 1956).
[vi] 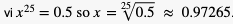 .
.
Andreoni, J. and C. Sprenger, (2012), 'Risk preferences are not time preferences', American Economic Review, 102 (7), 3357–76
Arrow, K. and M. Kurz (1970), Public Investment, the Rate of Return, and Optimal Fiscal Policy, Baltimore: Published for Resources for the Future by the Johns Hopkins Press
Cairns, J. (1994), 'Valuing future benefits', Health Economics, 3 (4), 221–29
Cropper, M., S. Aydede and P. Portney (1994), 'Preferences for life saving programs: How the public discounts time and age', Journal of Risk and Uncertainty, 8 (3), 243–65
Dasgupta, P. (2001), 'Valuing objects and evaluating policies in imperfect economies', The Economic Journal, 111 (471), C1–C29
Fisher, I. (1930), The Theory of Interest as Determined by Impatience to Spend Income and Opportunity to Invest it, New York: The Macmillan Company
Fontinelle, A. (2019), 'Standard of living vs. quality of life: What's the difference?', available at https://www.investopedia.com/articles/financial-theory/08/standard-of-living-quality-of-life.asp, accessed 8 May 2019
Frederick, S. (2003), 'Measuring intergenerational time preference: Are future lives valued less?', Journal of Risk and Uncertainty, 26 (1), 39–53
Johannesson, M. and P. Johansson (1997), 'Saving lives in the present versus saving lives in the future—Is there a framing effect?', Journal of Risk and Uncertainty, 15 (2), 167–76
Partnoy, F. (2012), Wait: The art and science of delay, New York: PublicAffairs
Pindyck, R. (2013), 'Climate change policy: What do the models tell us?', Journal of Economic Literature, 51 (3), 860–72
Poelhekke, S. (2017), 'Voor een optimale prijs is een CO2–belasting nodig', ESB, 102 (4754), 474–77
Schelling, T. (1995), 'Intergenerational discounting', Energy Policy, 23 (4), 395–401
Scherpenzeel, A. and M. Das (2010), '“True” longitudinal and probability-based internet panels: Evidence from the Netherlands', in Das, M., P. Ester and L. Kaczmirek (ed.), Social and Behavioral Research and the Internet: Advances in applied methods and research strategies, Boca Raton: Taylor & Francis, pp. 77–104
Schneider, D. (1968), American Kinship: A cultural account, Englewood Cliffs, NJ: Prentice-Hall
Statistics Netherlands (2014), 'Dutch quality of life is high, but not sustainable', available at https://www.cbs.nl/en-gb/news/2014/48/dutch-quality-of-life-is-high-but-not-sustainable, accessed 8 May 2019
Stern, N. H. (2007), The Stern Review of the Economics of Climate Change, Cambridge: Cambridge University Press
The Economist, (2018), 'The moral assumptions embedded in economic models of climate change', The Economist, 6 December 2018, available at https://www.economist.com/finance-and-economics/2018/12/06/the-moral-assumptions-embedded-in-economic-models-of-climate-change?fsrc=scn/tw/te/rfd/pe, accessed 8 May 2019
Benevolent social planner Hypothetical agent in full charge of society who executes exactly what its citizens (aggregately) request.
Cost–benefit analysis An investigation of costs and benefits of a potential project, often throughout several time periods. In this case, the discount factor becomes part of the analysis.
Constant exponential (discounting) Functional form of discounting that implies that the value of each delayed year relative to the previous year is the same, and equals the annual discount factor. The value of a multiple-period delay therefore shrinks exponentially. Examples of alternative forms are linear and hyperbolic discounting.
Discount factor Determines the valuation of something that is delayed to a future time period relative to its occurrence in the present.
Annual (discount factor) Discount factor for which the future time period is set one year from the present. Default term used in the discussion of discount factor values.
Discounting Valuing something that is delayed to a future time period relative to its occurrence in the present. If the value is less, then the future occurrence is ‘discounted’.
Intergenerational discounting See discounting. Distinct from both personal and social discounting because the unit that is delayed is carried over to another generation. Costs and benefits of a certain project might therefore not be borne by the same generation, thus complicating analysis.
Kinship In the natural sciences defined as ties to those with a genetical connection. This definition, rather than the non-genetical interpretation that is used in most social sciences, is the one of interest for this paper.
Monetary discounting See discounting. Special case of discounting for which the unit is money and the delay in principle only affects the agent who does the discounting.
Normative economics Discusses questions related to ‘what ought to be’.
Positive economics Discusses questions related to ‘what is’.
Public good In the pure form, this is any good from which no one can be excluded from consumption and consumption is non-rival, which means that the costs or scope of provision do not depend on the number of users. A public good is therefore well-suited to be provided by the public sector. Examples of such goods are streetlights, clean air and a healthy climate. Public goods can also be impure in which case they are still excludable or rival to some extent.
Risk preferences Human behaviour with respect to risk. In economics, three different risk preferences can be distinguished: risk-loving, risk-neutral and risk-averse types of people.
Social discounting See discounting. The valuation of the delayed (mostly public) unit is societal rather than individual.
Standard of life Measurement of well-being based on various indicators such as a person’s material resources, the structure of society and the (natural) environment.
Time discounting of life saving Valuing a number of lives saved in the future relative to a number of lives saved in the present. If these numbers are not equivalent, there exists time preference for saving lives.
Time preference Different term for (time) discounting.
Total utilitarianism Variant of utilitarianism in which the sum of all separate individual utilities needs to be maximised. This interpretation can be used to defend the importance of the utilities of those individuals not yet alive, since they similarly enter the total sum that needs to be maximised.
Welfare Measurement of well-being that classically focuses on material consumption. However, welfare is often used in a general comparison of well-being between different (groups of) people.
To cite this paper please use the following details: Voorintholt, L (2020), 'Discounting Beyond Death: An exploration of intergenerational distribution preferences', Reinvention: an International Journal of Undergraduate Research, Volume 13, Issue 1, https://reinventionjournal.org/article/view/491. Date accessed [insert date]. If you cite this article or use it in any teaching or other related activities please let us know by e-mailing us at Reinventionjournal@warwick.ac.uk.